Functions | |
| template<typename _Tp > | |
| __gnu_cxx::__promote< _Tp >::__type | __gnu_cxx::airy_ai (_Tp __x) |
| float | __gnu_cxx::airy_aif (float __x) |
| long double | __gnu_cxx::airy_ail (long double __x) |
| template<typename _Tp > | |
| __gnu_cxx::__promote< _Tp >::__type | __gnu_cxx::airy_bi (_Tp __x) |
| float | __gnu_cxx::airy_bif (float __x) |
| long double | __gnu_cxx::airy_bil (long double __x) |
| template<typename _Tp > | |
| __gnu_cxx::__promote< _Tp >::__type | std::assoc_laguerre (unsigned int __n, unsigned int __m, _Tp __x) |
| float | std::assoc_laguerref (unsigned int __n, unsigned int __m, float __x) |
| long double | std::assoc_laguerrel (unsigned int __n, unsigned int __m, long double __x) |
| template<typename _Tp > | |
| __gnu_cxx::__promote< _Tp >::__type | std::assoc_legendre (unsigned int __l, unsigned int __m, _Tp __x) |
| float | std::assoc_legendref (unsigned int __l, unsigned int __m, float __x) |
| long double | std::assoc_legendrel (unsigned int __l, unsigned int __m, long double __x) |
| template<typename _Tpa , typename _Tpb > | |
| __gnu_cxx::__promote_2< _Tpa, _Tpb >::__type | std::beta (_Tpa __a, _Tpb __b) |
| float | std::betaf (float __a, float __b) |
| long double | std::betal (long double __a, long double __b) |
| template<typename _Tp > | |
| __gnu_cxx::__promote< _Tp >::__type | std::comp_ellint_1 (_Tp __k) |
| float | std::comp_ellint_1f (float __k) |
| long double | std::comp_ellint_1l (long double __k) |
| template<typename _Tp > | |
| __gnu_cxx::__promote< _Tp >::__type | std::comp_ellint_2 (_Tp __k) |
| float | std::comp_ellint_2f (float __k) |
| long double | std::comp_ellint_2l (long double __k) |
| template<typename _Tp , typename _Tpn > | |
| __gnu_cxx::__promote_2< _Tp, _Tpn >::__type | std::comp_ellint_3 (_Tp __k, _Tpn __nu) |
| float | std::comp_ellint_3f (float __k, float __nu) |
| long double | std::comp_ellint_3l (long double __k, long double __nu) |
| template<typename _Tpa , typename _Tpc , typename _Tp > | |
| __gnu_cxx::__promote_3< _Tpa, _Tpc, _Tp >::__type | __gnu_cxx::conf_hyperg (_Tpa __a, _Tpc __c, _Tp __x) |
| float | __gnu_cxx::conf_hypergf (float __a, float __c, float __x) |
| long double | __gnu_cxx::conf_hypergl (long double __a, long double __c, long double __x) |
| template<typename _Tpnu , typename _Tp > | |
| __gnu_cxx::__promote_2< _Tpnu, _Tp >::__type | std::cyl_bessel_i (_Tpnu __nu, _Tp __x) |
| float | std::cyl_bessel_if (float __nu, float __x) |
| long double | std::cyl_bessel_il (long double __nu, long double __x) |
| template<typename _Tpnu , typename _Tp > | |
| __gnu_cxx::__promote_2< _Tpnu, _Tp >::__type | std::cyl_bessel_j (_Tpnu __nu, _Tp __x) |
| float | std::cyl_bessel_jf (float __nu, float __x) |
| long double | std::cyl_bessel_jl (long double __nu, long double __x) |
| template<typename _Tpnu , typename _Tp > | |
| __gnu_cxx::__promote_2< _Tpnu, _Tp >::__type | std::cyl_bessel_k (_Tpnu __nu, _Tp __x) |
| float | std::cyl_bessel_kf (float __nu, float __x) |
| long double | std::cyl_bessel_kl (long double __nu, long double __x) |
| template<typename _Tpnu , typename _Tp > | |
| __gnu_cxx::__promote_2< _Tpnu, _Tp >::__type | std::cyl_neumann (_Tpnu __nu, _Tp __x) |
| float | std::cyl_neumannf (float __nu, float __x) |
| long double | std::cyl_neumannl (long double __nu, long double __x) |
| template<typename _Tp , typename _Tpp > | |
| __gnu_cxx::__promote_2< _Tp, _Tpp >::__type | std::ellint_1 (_Tp __k, _Tpp __phi) |
| float | std::ellint_1f (float __k, float __phi) |
| long double | std::ellint_1l (long double __k, long double __phi) |
| template<typename _Tp , typename _Tpp > | |
| __gnu_cxx::__promote_2< _Tp, _Tpp >::__type | std::ellint_2 (_Tp __k, _Tpp __phi) |
| float | std::ellint_2f (float __k, float __phi) |
| long double | std::ellint_2l (long double __k, long double __phi) |
| template<typename _Tp , typename _Tpn , typename _Tpp > | |
| __gnu_cxx::__promote_3< _Tp, _Tpn, _Tpp >::__type | std::ellint_3 (_Tp __k, _Tpn __nu, _Tpp __phi) |
| float | std::ellint_3f (float __k, float __nu, float __phi) |
| long double | std::ellint_3l (long double __k, long double __nu, long double __phi) |
| template<typename _Tp > | |
| __gnu_cxx::__promote< _Tp >::__type | std::expint (_Tp __x) |
| float | std::expintf (float __x) |
| long double | std::expintl (long double __x) |
| template<typename _Tp > | |
| __gnu_cxx::__promote< _Tp >::__type | std::hermite (unsigned int __n, _Tp __x) |
| float | std::hermitef (unsigned int __n, float __x) |
| long double | std::hermitel (unsigned int __n, long double __x) |
| template<typename _Tpa , typename _Tpb , typename _Tpc , typename _Tp > | |
| __gnu_cxx::__promote_4< _Tpa, _Tpb, _Tpc, _Tp >::__type | __gnu_cxx::hyperg (_Tpa __a, _Tpb __b, _Tpc __c, _Tp __x) |
| float | __gnu_cxx::hypergf (float __a, float __b, float __c, float __x) |
| long double | __gnu_cxx::hypergl (long double __a, long double __b, long double __c, long double __x) |
| template<typename _Tp > | |
| __gnu_cxx::__promote< _Tp >::__type | std::laguerre (unsigned int __n, _Tp __x) |
| float | std::laguerref (unsigned int __n, float __x) |
| long double | std::laguerrel (unsigned int __n, long double __x) |
| template<typename _Tp > | |
| __gnu_cxx::__promote< _Tp >::__type | std::legendre (unsigned int __l, _Tp __x) |
| float | std::legendref (unsigned int __l, float __x) |
| long double | std::legendrel (unsigned int __l, long double __x) |
| template<typename _Tp > | |
| __gnu_cxx::__promote< _Tp >::__type | std::riemann_zeta (_Tp __s) |
| float | std::riemann_zetaf (float __s) |
| long double | std::riemann_zetal (long double __s) |
| template<typename _Tp > | |
| __gnu_cxx::__promote< _Tp >::__type | std::sph_bessel (unsigned int __n, _Tp __x) |
| float | std::sph_besself (unsigned int __n, float __x) |
| long double | std::sph_bessell (unsigned int __n, long double __x) |
| template<typename _Tp > | |
| __gnu_cxx::__promote< _Tp >::__type | std::sph_legendre (unsigned int __l, unsigned int __m, _Tp __theta) |
| float | std::sph_legendref (unsigned int __l, unsigned int __m, float __theta) |
| long double | std::sph_legendrel (unsigned int __l, unsigned int __m, long double __theta) |
| template<typename _Tp > | |
| __gnu_cxx::__promote< _Tp >::__type | std::sph_neumann (unsigned int __n, _Tp __x) |
| float | std::sph_neumannf (unsigned int __n, float __x) |
| long double | std::sph_neumannl (unsigned int __n, long double __x) |
Detailed Description
Mathematical Special Functions
A collection of advanced mathematical special functions, defined by ISO/IEC IS 29124 and then added to ISO C++ 2017.
Introduction and History
The first significant library upgrade on the road to C++2011, TR1, included a set of 23 mathematical functions that significantly extended the standard transcendental functions inherited from C and declared in <cmath>.
Although most components from TR1 were eventually adopted for C++11 these math functions were left behind out of concern for implementability. The math functions were published as a separate international standard IS 29124 - Extensions to the C++ Library to Support Mathematical Special Functions.
For C++17 these functions were incorporated into the main standard.
Contents
The following functions are implemented in namespace std:
- assoc_laguerre - Associated Laguerre functions
- assoc_legendre - Associated Legendre functions
- beta - Beta functions
- comp_ellint_1 - Complete elliptic functions of the first kind
- comp_ellint_2 - Complete elliptic functions of the second kind
- comp_ellint_3 - Complete elliptic functions of the third kind
- cyl_bessel_i - Regular modified cylindrical Bessel functions
- cyl_bessel_j - Cylindrical Bessel functions of the first kind
- cyl_bessel_k - Irregular modified cylindrical Bessel functions
- cyl_neumann - Cylindrical Neumann functions or Cylindrical Bessel functions of the second kind
- ellint_1 - Incomplete elliptic functions of the first kind
- ellint_2 - Incomplete elliptic functions of the second kind
- ellint_3 - Incomplete elliptic functions of the third kind
- expint - The exponential integral
- hermite - Hermite polynomials
- laguerre - Laguerre functions
- legendre - Legendre polynomials
- riemann_zeta - The Riemann zeta function
- sph_bessel - Spherical Bessel functions
- sph_legendre - Spherical Legendre functions
- sph_neumann - Spherical Neumann functions
The hypergeometric functions were stricken from the TR29124 and C++17 versions of this math library because of implementation concerns. However, since they were in the TR1 version and since they are popular we kept them as an extension in namespace __gnu_cxx:
Argument Promotion
The arguments suppled to the non-suffixed functions will be promoted according to the following rules:
- If any argument intended to be floating point is given an integral value That integral value is promoted to double.
- All floating point arguments are promoted up to the largest floating point precision among them.
NaN Arguments
If any of the floating point arguments supplied to these functions is invalid or NaN (std::numeric_limits<Tp>::quiet_NaN), the value NaN is returned.
Implementation
We strive to implement the underlying math with type generic algorithms to the greatest extent possible. In practice, the functions are thin wrappers that dispatch to function templates. Type dependence is controlled with std::numeric_limits and functions thereof.
We don't promote float to double or double to long double reflexively. The goal is for float functions to operate more quickly, at the cost of float accuracy and possibly a smaller domain of validity. Similaryly, long double should give you more dynamic range and slightly more pecision than double on many systems.
Testing
These functions have been tested against equivalent implementations from the Gnu Scientific Library, GSL and Boost and the ratio
![\[
\frac{|f - f_{test}|}{|f_{test}|}
\]](form_40.png)
is generally found to be within 10-15 for 64-bit double on linux-x86_64 systems over most of the ranges of validity.
- Todo:
- Provide accuracy comparisons on a per-function basis for a small number of targets.
General Bibliography
- See also
- Abramowitz and Stegun: Handbook of Mathematical Functions, with Formulas, Graphs, and Mathematical Tables Edited by Milton Abramowitz and Irene A. Stegun, National Bureau of Standards Applied Mathematics Series - 55 Issued June 1964, Tenth Printing, December 1972, with corrections Electronic versions of A&S abound including both pdf and navigable html.
- for example http://people.math.sfu.ca/~cbm/aands/
- The old A&S has been redone as the NIST Digital Library of Mathematical Functions: http://dlmf.nist.gov/ This version is far more navigable and includes more recent work.
- An Atlas of Functions: with Equator, the Atlas Function Calculator 2nd Edition, by Oldham, Keith B., Myland, Jan, Spanier, Jerome
- Asymptotics and Special Functions by Frank W. J. Olver, Academic Press, 1974
- Numerical Recipes in C, The Art of Scientific Computing, by William H. Press, Second Ed., Saul A. Teukolsky, William T. Vetterling, and Brian P. Flannery, Cambridge University Press, 1992
- The Special Functions and Their Approximations: Volumes 1 and 2, by Yudell L. Luke, Academic Press, 1969
Function Documentation
◆ airy_ai()
|
inline |
◆ airy_aif()
|
inline |
◆ airy_ail()
|
inline |
◆ airy_bi()
|
inline |
◆ airy_bif()
|
inline |
◆ airy_bil()
|
inline |
◆ assoc_laguerre()
|
inline |
Return the associated Laguerre polynomial of nonnegative order n, nonnegative degree m and real argument x: 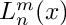
The associated Laguerre function of real degree 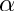
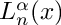
![\[
L_n^\alpha(x) = \frac{(\alpha + 1)_n}{n!}
{}_1F_1(-n; \alpha + 1; x)
\]](form_44.png)
where 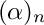
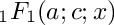
The associated Laguerre polynomial is defined for integral degree 
![\[
L_n^m(x) = (-1)^m \frac{d^m}{dx^m} L_{n + m}(x)
\]](form_48.png)
where the Laguerre polynomial is defined by:
![\[
L_n(x) = \frac{e^x}{n!} \frac{d^n}{dx^n} (x^ne^{-x})
\]](form_49.png)
and 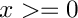
- See also
- laguerre for details of the Laguerre function of degree
n
- Template Parameters
-
_Tp The floating-point type of the argument __x.
- Parameters
-
__n The order of the Laguerre function, __n >= 0.__m The degree of the Laguerre function, __m >= 0.__x The argument of the Laguerre function, __x >= 0.
- Exceptions
-
std::domain_error if __x < 0.
◆ assoc_laguerref()
|
inline |
◆ assoc_laguerrel()
|
inline |
◆ assoc_legendre()
|
inline |
Return the associated Legendre function of degree l and order m.
The associated Legendre function is derived from the Legendre function 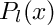
![\[
P_l^m(x) = (1 - x^2)^{m/2}\frac{d^m}{dx^m}P_l(x)
\]](form_52.png)
- See also
- legendre for details of the Legendre function of degree
l
- Template Parameters
-
_Tp The floating-point type of the argument __x.
- Parameters
-
__l The degree __l >= 0.__m The order __m <= l.__x The argument, abs(__x) <= 1.
- Exceptions
-
std::domain_error if abs(__x) > 1.
◆ assoc_legendref()
|
inline |
◆ assoc_legendrel()
|
inline |
◆ beta()
|
inline |
Return the beta function, 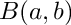
a, b.
The beta function is defined by
![\[
B(a,b) = \int_0^1 t^{a - 1} (1 - t)^{b - 1} dt
= \frac{\Gamma(a)\Gamma(b)}{\Gamma(a+b)}
\]](form_55.png)
where 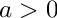
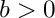
- Template Parameters
-
_Tpa The floating-point type of the parameter __a._Tpb The floating-point type of the parameter __b.
- Parameters
-
__a The first argument of the beta function, __a > 0.__b The second argument of the beta function, __b > 0.
- Exceptions
-
std::domain_error if __a < 0or__b < 0.
◆ betaf()
|
inline |
◆ betal()
|
inline |
◆ comp_ellint_1()
|
inline |
Return the complete elliptic integral of the first kind 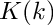
k.
The complete elliptic integral of the first kind is defined as
![\[
K(k) = F(k,\pi/2) = \int_0^{\pi/2}\frac{d\theta}
{\sqrt{1 - k^2 sin^2\theta}}
\]](form_60.png)
where 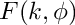
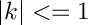
- See also
- ellint_1 for details of the incomplete elliptic function of the first kind.
- Template Parameters
-
_Tp The floating-point type of the modulus __k.
- Parameters
-
__k The modulus, abs(__k) <= 1
- Exceptions
-
std::domain_error if abs(__k) > 1.
◆ comp_ellint_1f()
|
inline |
◆ comp_ellint_1l()
|
inline |
◆ comp_ellint_2()
|
inline |
Return the complete elliptic integral of the second kind 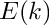
k.
The complete elliptic integral of the second kind is defined as
![\[
E(k) = E(k,\pi/2) = \int_0^{\pi/2}\sqrt{1 - k^2 sin^2\theta}
\]](form_63.png)
where 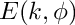
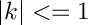
- See also
- ellint_2 for details of the incomplete elliptic function of the second kind.
- Template Parameters
-
_Tp The floating-point type of the modulus __k.
- Parameters
-
__k The modulus, abs(__k)<= 1
- Exceptions
-
std::domain_error if abs(__k)> 1.
◆ comp_ellint_2f()
|
inline |
◆ comp_ellint_2l()
|
inline |
◆ comp_ellint_3()
|
inline |
Return the complete elliptic integral of the third kind 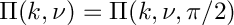
k.
The complete elliptic integral of the third kind is defined as
![\[
\Pi(k,\nu) = \Pi(k,\nu,\pi/2) = \int_0^{\pi/2}
\frac{d\theta}
{(1 - \nu \sin^2\theta)\sqrt{1 - k^2 \sin^2\theta}}
\]](form_67.png)
where 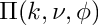
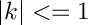
- See also
- ellint_3 for details of the incomplete elliptic function of the third kind.
- Template Parameters
-
_Tp The floating-point type of the modulus __k._Tpn The floating-point type of the argument __nu.
- Parameters
-
__k The modulus, abs(__k)<= 1__nu The argument
- Exceptions
-
std::domain_error if abs(__k)> 1.
◆ comp_ellint_3f()
|
inline |
◆ comp_ellint_3l()
|
inline |
◆ conf_hyperg()
|
inline |
Return the confluent hypergeometric function 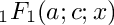
a, denominatorial parameter c, and argument x.
The confluent hypergeometric function is defined by
![\[
{}_1F_1(a;c;x) = \sum_{n=0}^{\infty} \frac{(a)_n x^n}{(c)_n n!}
\]](form_112.png)
where the Pochhammer symbol is 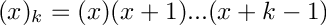
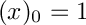
- Parameters
-
__a The numeratorial parameter __c The denominatorial parameter __x The argument
◆ conf_hypergf()
|
inline |
◆ conf_hypergl()
|
inline |
◆ cyl_bessel_i()
|
inline |
Return the regular modified Bessel function 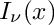
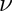
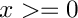
The regular modified cylindrical Bessel function is:
![\[
I_{\nu}(x) = i^{-\nu}J_\nu(ix) = \sum_{k=0}^{\infty}
\frac{(x/2)^{\nu + 2k}}{k!\Gamma(\nu+k+1)}
\]](form_71.png)
- Template Parameters
-
_Tpnu The floating-point type of the order __nu._Tp The floating-point type of the argument __x.
- Parameters
-
__nu The order __x The argument, __x >= 0
- Exceptions
-
std::domain_error if __x < 0.
◆ cyl_bessel_if()
|
inline |
◆ cyl_bessel_il()
|
inline |
◆ cyl_bessel_j()
|
inline |
Return the Bessel function 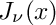
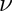
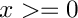
The cylindrical Bessel function is:
![\[
J_{\nu}(x) = \sum_{k=0}^{\infty}
\frac{(-1)^k (x/2)^{\nu + 2k}}{k!\Gamma(\nu+k+1)}
\]](form_73.png)
- Template Parameters
-
_Tpnu The floating-point type of the order __nu._Tp The floating-point type of the argument __x.
- Parameters
-
__nu The order __x The argument, __x >= 0
- Exceptions
-
std::domain_error if __x < 0.
◆ cyl_bessel_jf()
|
inline |
◆ cyl_bessel_jl()
|
inline |
◆ cyl_bessel_k()
|
inline |
Return the irregular modified Bessel function 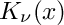
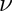
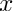
The irregular modified Bessel function is defined by:
![\[
K_{\nu}(x) = \frac{\pi}{2}
\frac{I_{-\nu}(x) - I_{\nu}(x)}{\sin \nu\pi}
\]](form_76.png)
where for integral 
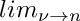
![\[
K_{-\nu}(x) = K_{\nu}(x)
\]](form_79.png)
- Template Parameters
-
_Tpnu The floating-point type of the order __nu._Tp The floating-point type of the argument __x.
- Parameters
-
__nu The order __x The argument, __x >= 0
- Exceptions
-
std::domain_error if __x < 0.
◆ cyl_bessel_kf()
|
inline |
◆ cyl_bessel_kl()
|
inline |
◆ cyl_neumann()
|
inline |
Return the Neumann function 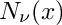
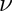
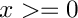
The Neumann function is defined by:
![\[
N_{\nu}(x) = \frac{J_{\nu}(x) \cos \nu\pi - J_{-\nu}(x)}
{\sin \nu\pi}
\]](form_81.png)
where 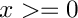

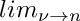
- Template Parameters
-
_Tpnu The floating-point type of the order __nu._Tp The floating-point type of the argument __x.
- Parameters
-
__nu The order __x The argument, __x >= 0
- Exceptions
-
std::domain_error if __x < 0.
◆ cyl_neumannf()
|
inline |
◆ cyl_neumannl()
|
inline |
◆ ellint_1()
|
inline |
Return the incomplete elliptic integral of the first kind 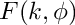
real modulus 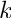
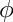
The incomplete elliptic integral of the first kind is defined as
![\[
F(k,\phi) = \int_0^{\phi}\frac{d\theta}
{\sqrt{1 - k^2 sin^2\theta}}
\]](form_84.png)
For 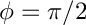
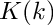
- See also
- comp_ellint_1.
- Template Parameters
-
_Tp The floating-point type of the modulus __k._Tpp The floating-point type of the angle __phi.
- Parameters
-
__k The modulus, abs(__k) <= 1__phi The integral limit argument in radians
- Exceptions
-
std::domain_error if abs(__k) > 1.
◆ ellint_1f()
|
inline |
◆ ellint_1l()
|
inline |
◆ ellint_2()
|
inline |
Return the incomplete elliptic integral of the second kind 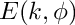
The incomplete elliptic integral of the second kind is defined as
![\[
E(k,\phi) = \int_0^{\phi} \sqrt{1 - k^2 sin^2\theta}
\]](form_86.png)
For 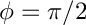
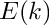
- See also
- comp_ellint_2.
- Template Parameters
-
_Tp The floating-point type of the modulus __k._Tpp The floating-point type of the angle __phi.
- Parameters
-
__k The modulus, abs(__k) <= 1__phi The integral limit argument in radians
- Returns
- The elliptic function of the second kind.
- Exceptions
-
std::domain_error if abs(__k) > 1.
◆ ellint_2f()
|
inline |
◆ ellint_2l()
|
inline |
◆ ellint_3()
|
inline |
Return the incomplete elliptic integral of the third kind 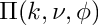
The incomplete elliptic integral of the third kind is defined by:
![\[
\Pi(k,\nu,\phi) = \int_0^{\phi}
\frac{d\theta}
{(1 - \nu \sin^2\theta)
\sqrt{1 - k^2 \sin^2\theta}}
\]](form_87.png)
For 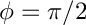
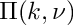
- See also
- comp_ellint_3.
- Template Parameters
-
_Tp The floating-point type of the modulus __k._Tpn The floating-point type of the argument __nu._Tpp The floating-point type of the angle __phi.
- Parameters
-
__k The modulus, abs(__k) <= 1__nu The second argument __phi The integral limit argument in radians
- Returns
- The elliptic function of the third kind.
- Exceptions
-
std::domain_error if abs(__k) > 1.
◆ ellint_3f()
|
inline |
◆ ellint_3l()
|
inline |
◆ expint()
|
inline |
◆ expintf()
|
inline |
◆ expintl()
|
inline |
◆ hermite()
|
inline |
Return the Hermite polynomial 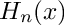
real argument x.
The Hermite polynomial is defined by:
![\[
H_n(x) = (-1)^n e^{x^2} \frac{d^n}{dx^n} e^{-x^2}
\]](form_91.png)
The Hermite polynomial obeys a reflection formula:
![\[
H_n(-x) = (-1)^n H_n(x)
\]](form_92.png)
- Template Parameters
-
_Tp The floating-point type of the argument __x.
- Parameters
-
__n The order __x The argument
◆ hermitef()
|
inline |
◆ hermitel()
|
inline |
◆ hyperg()
|
inline |
Return the hypergeometric function 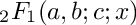
a and b, denominatorial parameter c, and argument x.
The hypergeometric function is defined by
![\[
{}_2F_1(a;c;x) = \sum_{n=0}^{\infty} \frac{(a)_n (b)_n x^n}{(c)_n n!}
\]](form_116.png)
where the Pochhammer symbol is 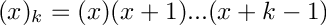
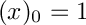
- Parameters
-
__a The first numeratorial parameter __b The second numeratorial parameter __c The denominatorial parameter __x The argument
◆ hypergf()
|
inline |
◆ hypergl()
|
inline |
◆ laguerre()
|
inline |
Returns the Laguerre polynomial 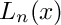
n and real argument 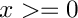
The Laguerre polynomial is defined by:
![\[
L_n(x) = \frac{e^x}{n!} \frac{d^n}{dx^n} (x^ne^{-x})
\]](form_49.png)
- Template Parameters
-
_Tp The floating-point type of the argument __x.
- Parameters
-
__n The nonnegative order __x The argument __x >= 0
- Exceptions
-
std::domain_error if __x < 0.
◆ laguerref()
|
inline |
◆ laguerrel()
|
inline |
◆ legendre()
|
inline |
Return the Legendre polynomial 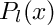
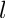
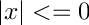
The Legendre function of order 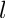
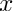
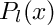
![\[
P_l(x) = \frac{1}{2^l l!}\frac{d^l}{dx^l}(x^2 - 1)^{l}
\]](form_96.png)
- Template Parameters
-
_Tp The floating-point type of the argument __x.
- Parameters
-
__l The degree 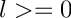
__x The argument abs(__x)<= 1
- Exceptions
-
std::domain_error if abs(__x)> 1
◆ legendref()
|
inline |
◆ legendrel()
|
inline |
◆ riemann_zeta()
|
inline |
◆ riemann_zetaf()
|
inline |
◆ riemann_zetal()
|
inline |
◆ sph_bessel()
|
inline |
Return the spherical Bessel function 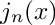
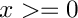
The spherical Bessel function is defined by:
![\[
j_n(x) = \left(\frac{\pi}{2x} \right) ^{1/2} J_{n+1/2}(x)
\]](form_104.png)
- Template Parameters
-
_Tp The floating-point type of the argument __x.
- Parameters
-
__n The integral order n >= 0__x The real argument x >= 0
- Exceptions
-
std::domain_error if __x < 0.
◆ sph_besself()
|
inline |
◆ sph_bessell()
|
inline |
◆ sph_legendre()
|
inline |
Return the spherical Legendre function of nonnegative integral degree l and order m and real angle 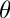
The spherical Legendre function is defined by
![\[
Y_l^m(\theta,\phi) = (-1)^m[\frac{(2l+1)}{4\pi}
\frac{(l-m)!}{(l+m)!}]
P_l^m(\cos\theta) \exp^{im\phi}
\]](form_106.png)
- Template Parameters
-
_Tp The floating-point type of the angle __theta.
- Parameters
-
__l The order __l >= 0__m The degree __m >= 0and__m <= __l__theta The radian polar angle argument
◆ sph_legendref()
|
inline |
◆ sph_legendrel()
|
inline |
◆ sph_neumann()
|
inline |
Return the spherical Neumann function of integral order 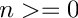
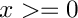
The spherical Neumann function is defined by
![\[
n_n(x) = \left(\frac{\pi}{2x} \right) ^{1/2} N_{n+1/2}(x)
\]](form_108.png)
- Template Parameters
-
_Tp The floating-point type of the argument __x.
- Parameters
-
__n The integral order n >= 0__x The real argument __x >= 0
- Exceptions
-
std::domain_error if __x < 0.
◆ sph_neumannf()
|
inline |
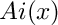
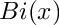
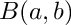
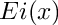
![\[
Ei(x) = -\int_{-x}^\infty \frac{e^t}{t} dt
\]](form_89.png)
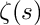
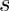
![\[
\zeta(s) = \sum_{k=1}^{\infty} k^{-s} \hbox{ for } s > 1
\]](form_100.png)
![\[
\zeta(s) = \frac{1}{1-2^{1-s}}\sum_{k=1}^{\infty}(-1)^{k-1}k^{-s}
\hbox{ for } 0 <= s <= 1
\]](form_101.png)
![\[
\zeta(s) = 2^s \pi^{s-1} \sin(\frac{\pi s}{2}) \Gamma(1-s) \zeta(1-s)
\]](form_102.png)