Functions | |
| template<typename _Tp > | |
| __gnu_cxx::__promote< _Tp >::__type | std::assoc_laguerre (unsigned int __n, unsigned int __m, _Tp __x) |
| float | std::assoc_laguerref (unsigned int __n, unsigned int __m, float __x) |
| long double | std::assoc_laguerrel (unsigned int __n, unsigned int __m, long double __x) |
| template<typename _Tp > | |
| __gnu_cxx::__promote< _Tp >::__type | std::assoc_legendre (unsigned int __l, unsigned int __m, _Tp __x) |
| float | std::assoc_legendref (unsigned int __l, unsigned int __m, float __x) |
| long double | std::assoc_legendrel (unsigned int __l, unsigned int __m, long double __x) |
| template<typename _Tpa , typename _Tpb > | |
| __gnu_cxx::__promote_2< _Tpa, _Tpb >::__type | std::beta (_Tpa __a, _Tpb __b) |
| float | std::betaf (float __a, float __b) |
| long double | std::betal (long double __a, long double __b) |
| template<typename _Tp > | |
| __gnu_cxx::__promote< _Tp >::__type | std::comp_ellint_1 (_Tp __k) |
| float | std::comp_ellint_1f (float __k) |
| long double | std::comp_ellint_1l (long double __k) |
| template<typename _Tp > | |
| __gnu_cxx::__promote< _Tp >::__type | std::comp_ellint_2 (_Tp __k) |
| float | std::comp_ellint_2f (float __k) |
| long double | std::comp_ellint_2l (long double __k) |
| template<typename _Tp , typename _Tpn > | |
| __gnu_cxx::__promote_2< _Tp, _Tpn >::__type | std::comp_ellint_3 (_Tp __k, _Tpn __nu) |
| float | std::comp_ellint_3f (float __k, float __nu) |
| long double | std::comp_ellint_3l (long double __k, long double __nu) |
| template<typename _Tpnu , typename _Tp > | |
| __gnu_cxx::__promote_2< _Tpnu, _Tp >::__type | std::cyl_bessel_i (_Tpnu __nu, _Tp __x) |
| float | std::cyl_bessel_if (float __nu, float __x) |
| long double | std::cyl_bessel_il (long double __nu, long double __x) |
| template<typename _Tpnu , typename _Tp > | |
| __gnu_cxx::__promote_2< _Tpnu, _Tp >::__type | std::cyl_bessel_j (_Tpnu __nu, _Tp __x) |
| float | std::cyl_bessel_jf (float __nu, float __x) |
| long double | std::cyl_bessel_jl (long double __nu, long double __x) |
| template<typename _Tpnu , typename _Tp > | |
| __gnu_cxx::__promote_2< _Tpnu, _Tp >::__type | std::cyl_bessel_k (_Tpnu __nu, _Tp __x) |
| float | std::cyl_bessel_kf (float __nu, float __x) |
| long double | std::cyl_bessel_kl (long double __nu, long double __x) |
| template<typename _Tpnu , typename _Tp > | |
| __gnu_cxx::__promote_2< _Tpnu, _Tp >::__type | std::cyl_neumann (_Tpnu __nu, _Tp __x) |
| float | std::cyl_neumannf (float __nu, float __x) |
| long double | std::cyl_neumannl (long double __nu, long double __x) |
| template<typename _Tp , typename _Tpp > | |
| __gnu_cxx::__promote_2< _Tp, _Tpp >::__type | std::ellint_1 (_Tp __k, _Tpp __phi) |
| float | std::ellint_1f (float __k, float __phi) |
| long double | std::ellint_1l (long double __k, long double __phi) |
| template<typename _Tp , typename _Tpp > | |
| __gnu_cxx::__promote_2< _Tp, _Tpp >::__type | std::ellint_2 (_Tp __k, _Tpp __phi) |
| float | std::ellint_2f (float __k, float __phi) |
| long double | std::ellint_2l (long double __k, long double __phi) |
| template<typename _Tp , typename _Tpn , typename _Tpp > | |
| __gnu_cxx::__promote_3< _Tp, _Tpn, _Tpp >::__type | std::ellint_3 (_Tp __k, _Tpn __nu, _Tpp __phi) |
| float | std::ellint_3f (float __k, float __nu, float __phi) |
| long double | std::ellint_3l (long double __k, long double __nu, long double __phi) |
| template<typename _Tp > | |
| __gnu_cxx::__promote< _Tp >::__type | std::expint (_Tp __x) |
| float | std::expintf (float __x) |
| long double | std::expintl (long double __x) |
| template<typename _Tp > | |
| __gnu_cxx::__promote< _Tp >::__type | std::hermite (unsigned int __n, _Tp __x) |
| float | std::hermitef (unsigned int __n, float __x) |
| long double | std::hermitel (unsigned int __n, long double __x) |
| template<typename _Tp > | |
| __gnu_cxx::__promote< _Tp >::__type | std::laguerre (unsigned int __n, _Tp __x) |
| float | std::laguerref (unsigned int __n, float __x) |
| long double | std::laguerrel (unsigned int __n, long double __x) |
| template<typename _Tp > | |
| __gnu_cxx::__promote< _Tp >::__type | std::legendre (unsigned int __l, _Tp __x) |
| float | std::legendref (unsigned int __l, float __x) |
| long double | std::legendrel (unsigned int __l, long double __x) |
| template<typename _Tp > | |
| __gnu_cxx::__promote< _Tp >::__type | std::riemann_zeta (_Tp __s) |
| float | std::riemann_zetaf (float __s) |
| long double | std::riemann_zetal (long double __s) |
| template<typename _Tp > | |
| __gnu_cxx::__promote< _Tp >::__type | std::sph_bessel (unsigned int __n, _Tp __x) |
| float | std::sph_besself (unsigned int __n, float __x) |
| long double | std::sph_bessell (unsigned int __n, long double __x) |
| template<typename _Tp > | |
| __gnu_cxx::__promote< _Tp >::__type | std::sph_legendre (unsigned int __l, unsigned int __m, _Tp __theta) |
| float | std::sph_legendref (unsigned int __l, unsigned int __m, float __theta) |
| long double | std::sph_legendrel (unsigned int __l, unsigned int __m, long double __theta) |
| template<typename _Tp > | |
| __gnu_cxx::__promote< _Tp >::__type | std::sph_neumann (unsigned int __n, _Tp __x) |
| float | std::sph_neumannf (unsigned int __n, float __x) |
| long double | std::sph_neumannl (unsigned int __n, long double __x) |
Detailed Description
A collection of advanced mathematical special functions, defined by ISO/IEC IS 29124.
Function Documentation
|
inline |
Return the associated Laguerre polynomial of nonnegative order n, nonnegative degree m and real argument x: 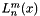 .
.
The associated Laguerre function of real degree 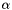 ,
, 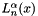 , is defined by
, is defined by
![\[ L_n^\alpha(x) = \frac{(\alpha + 1)_n}{n!} {}_1F_1(-n; \alpha + 1; x) \]](form_44.png)
where 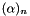 is the Pochhammer symbol and
is the Pochhammer symbol and 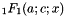 is the confluent hypergeometric function.
is the confluent hypergeometric function.
The associated Laguerre polynomial is defined for integral degree  by:
by:
![\[ L_n^m(x) = (-1)^m \frac{d^m}{dx^m} L_{n + m}(x) \]](form_48.png)
where the Laguerre polynomial is defined by:
![\[ L_n(x) = \frac{e^x}{n!} \frac{d^n}{dx^n} (x^ne^{-x}) \]](form_49.png)
and 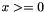 .
.
- See also
- laguerre for details of the Laguerre function of degree
n
- Template Parameters
-
_Tp The floating-point type of the argument __x.
- Parameters
-
__n The order of the Laguerre function, __n >= 0.__m The degree of the Laguerre function, __m >= 0.__x The argument of the Laguerre function, __x >= 0.
- Exceptions
-
std::domain_error if __x < 0.
|
inline |
|
inline |
|
inline |
Return the associated Legendre function of degree l and order m.
The associated Legendre function is derived from the Legendre function 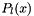 by the Rodrigues formula:
by the Rodrigues formula:
![\[ P_l^m(x) = (1 - x^2)^{m/2}\frac{d^m}{dx^m}P_l(x) \]](form_52.png)
- See also
- legendre for details of the Legendre function of degree
l
- Template Parameters
-
_Tp The floating-point type of the argument __x.
- Parameters
-
__l The degree __l >= 0.__m The order __m <= l.__x The argument, abs(__x) <= 1.
- Exceptions
-
std::domain_error if abs(__x) > 1.
|
inline |
|
inline |
|
inline |
Return the beta function, 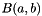 , for real parameters
, for real parameters a, b.
The beta function is defined by
![\[ B(a,b) = \int_0^1 t^{a - 1} (1 - t)^{b - 1} dt = \frac{\Gamma(a)\Gamma(b)}{\Gamma(a+b)} \]](form_55.png)
where 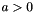 and
and 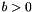
- Template Parameters
-
_Tpa The floating-point type of the parameter __a._Tpb The floating-point type of the parameter __b.
- Parameters
-
__a The first argument of the beta function, __a > 0.__b The second argument of the beta function, __b > 0.
- Exceptions
-
std::domain_error if __a < 0or__b < 0.
|
inline |
|
inline |
|
inline |
Return the complete elliptic integral of the first kind 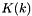 for real modulus
for real modulus k.
The complete elliptic integral of the first kind is defined as
![\[ K(k) = F(k,\pi/2) = \int_0^{\pi/2}\frac{d\theta} {\sqrt{1 - k^2 sin^2\theta}} \]](form_60.png)
where 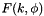 is the incomplete elliptic integral of the first kind and the modulus
is the incomplete elliptic integral of the first kind and the modulus 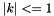 .
.
- See also
- ellint_1 for details of the incomplete elliptic function of the first kind.
- Template Parameters
-
_Tp The floating-point type of the modulus __k.
- Parameters
-
__k The modulus, abs(__k) <= 1
- Exceptions
-
std::domain_error if abs(__k) > 1.
|
inline |
|
inline |
|
inline |
Return the complete elliptic integral of the second kind 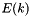 for real modulus
for real modulus k.
The complete elliptic integral of the second kind is defined as
![\[ E(k) = E(k,\pi/2) = \int_0^{\pi/2}\sqrt{1 - k^2 sin^2\theta} \]](form_63.png)
where 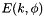 is the incomplete elliptic integral of the second kind and the modulus
is the incomplete elliptic integral of the second kind and the modulus 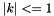 .
.
- See also
- ellint_2 for details of the incomplete elliptic function of the second kind.
- Template Parameters
-
_Tp The floating-point type of the modulus __k.
- Parameters
-
__k The modulus, abs(__k)<= 1
- Exceptions
-
std::domain_error if abs(__k)> 1.
|
inline |
|
inline |
|
inline |
Return the complete elliptic integral of the third kind 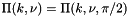 for real modulus
for real modulus k.
The complete elliptic integral of the third kind is defined as
![\[ \Pi(k,\nu) = \Pi(k,\nu,\pi/2) = \int_0^{\pi/2} \frac{d\theta} {(1 - \nu \sin^2\theta)\sqrt{1 - k^2 \sin^2\theta}} \]](form_67.png)
where 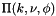 is the incomplete elliptic integral of the second kind and the modulus
is the incomplete elliptic integral of the second kind and the modulus 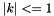 .
.
- See also
- ellint_3 for details of the incomplete elliptic function of the third kind.
- Template Parameters
-
_Tp The floating-point type of the modulus __k._Tpn The floating-point type of the argument __nu.
- Parameters
-
__k The modulus, abs(__k)<= 1__nu The argument
- Exceptions
-
std::domain_error if abs(__k)> 1.
|
inline |
|
inline |
|
inline |
Return the regular modified Bessel function 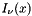 for real order
for real order 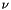 and argument
and argument 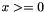 .
.
The regular modified cylindrical Bessel function is:
![\[ I_{\nu}(x) = i^{-\nu}J_\nu(ix) = \sum_{k=0}^{\infty} \frac{(x/2)^{\nu + 2k}}{k!\Gamma(\nu+k+1)} \]](form_71.png)
- Template Parameters
-
_Tpnu The floating-point type of the order __nu._Tp The floating-point type of the argument __x.
- Parameters
-
__nu The order __x The argument, __x >= 0
- Exceptions
-
std::domain_error if __x < 0.
|
inline |
|
inline |
|
inline |
Return the Bessel function 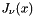 of real order
of real order 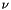 and argument
and argument 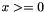 .
.
The cylindrical Bessel function is:
![\[ J_{\nu}(x) = \sum_{k=0}^{\infty} \frac{(-1)^k (x/2)^{\nu + 2k}}{k!\Gamma(\nu+k+1)} \]](form_73.png)
- Template Parameters
-
_Tpnu The floating-point type of the order __nu._Tp The floating-point type of the argument __x.
- Parameters
-
__nu The order __x The argument, __x >= 0
- Exceptions
-
std::domain_error if __x < 0.
|
inline |
|
inline |
|
inline |
Return the irregular modified Bessel function 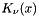 of real order
of real order 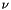 and argument
and argument 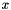 .
.
The irregular modified Bessel function is defined by:
![\[ K_{\nu}(x) = \frac{\pi}{2} \frac{I_{-\nu}(x) - I_{\nu}(x)}{\sin \nu\pi} \]](form_76.png)
where for integral 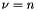 a limit is taken:
a limit is taken: 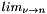 . For negative argument we have simply:
. For negative argument we have simply:
![\[ K_{-\nu}(x) = K_{\nu}(x) \]](form_79.png)
- Template Parameters
-
_Tpnu The floating-point type of the order __nu._Tp The floating-point type of the argument __x.
- Parameters
-
__nu The order __x The argument, __x >= 0
- Exceptions
-
std::domain_error if __x < 0.
|
inline |
|
inline |
|
inline |
Return the Neumann function 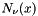 of real order
of real order 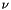 and argument
and argument 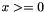 .
.
The Neumann function is defined by:
![\[ N_{\nu}(x) = \frac{J_{\nu}(x) \cos \nu\pi - J_{-\nu}(x)} {\sin \nu\pi} \]](form_81.png)
where 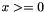 and for integral order
and for integral order 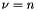 a limit is taken:
a limit is taken: 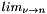 .
.
- Template Parameters
-
_Tpnu The floating-point type of the order __nu._Tp The floating-point type of the argument __x.
- Parameters
-
__nu The order __x The argument, __x >= 0
- Exceptions
-
std::domain_error if __x < 0.
|
inline |
|
inline |
|
inline |
Return the incomplete elliptic integral of the first kind 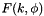 for
for real modulus 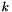 and angle
and angle 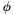 .
.
The incomplete elliptic integral of the first kind is defined as
![\[ F(k,\phi) = \int_0^{\phi}\frac{d\theta} {\sqrt{1 - k^2 sin^2\theta}} \]](form_84.png)
For 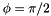 this becomes the complete elliptic integral of the first kind,
this becomes the complete elliptic integral of the first kind, 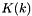 .
.
- See also
- comp_ellint_1.
- Template Parameters
-
_Tp The floating-point type of the modulus __k._Tpp The floating-point type of the angle __phi.
- Parameters
-
__k The modulus, abs(__k) <= 1__phi The integral limit argument in radians
- Exceptions
-
std::domain_error if abs(__k) > 1.
|
inline |
|
inline |
|
inline |
Return the incomplete elliptic integral of the second kind 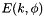 .
.
The incomplete elliptic integral of the second kind is defined as
![\[ E(k,\phi) = \int_0^{\phi} \sqrt{1 - k^2 sin^2\theta} \]](form_86.png)
For 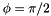 this becomes the complete elliptic integral of the second kind,
this becomes the complete elliptic integral of the second kind, 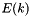 .
.
- See also
- comp_ellint_2.
- Template Parameters
-
_Tp The floating-point type of the modulus __k._Tpp The floating-point type of the angle __phi.
- Parameters
-
__k The modulus, abs(__k) <= 1__phi The integral limit argument in radians
- Returns
- The elliptic function of the second kind.
- Exceptions
-
std::domain_error if abs(__k) > 1.
|
inline |
|
inline |
|
inline |
Return the incomplete elliptic integral of the third kind 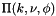 .
.
The incomplete elliptic integral of the third kind is defined by:
![\[ \Pi(k,\nu,\phi) = \int_0^{\phi} \frac{d\theta} {(1 - \nu \sin^2\theta) \sqrt{1 - k^2 \sin^2\theta}} \]](form_87.png)
For 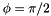 this becomes the complete elliptic integral of the third kind,
this becomes the complete elliptic integral of the third kind, 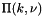 .
.
- See also
- comp_ellint_3.
- Template Parameters
-
_Tp The floating-point type of the modulus __k._Tpn The floating-point type of the argument __nu._Tpp The floating-point type of the angle __phi.
- Parameters
-
__k The modulus, abs(__k) <= 1__nu The second argument __phi The integral limit argument in radians
- Returns
- The elliptic function of the third kind.
- Exceptions
-
std::domain_error if abs(__k) > 1.
|
inline |
|
inline |
|
inline |
|
inline |
|
inline |
|
inline |
Return the Hermite polynomial 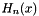 of order n and
of order n and real argument x.
The Hermite polynomial is defined by:
![\[ H_n(x) = (-1)^n e^{x^2} \frac{d^n}{dx^n} e^{-x^2} \]](form_91.png)
The Hermite polynomial obeys a reflection formula:
![\[ H_n(-x) = (-1)^n H_n(x) \]](form_92.png)
- Template Parameters
-
_Tp The floating-point type of the argument __x.
- Parameters
-
__n The order __x The argument
|
inline |
|
inline |
|
inline |
Returns the Laguerre polynomial 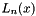 of nonnegative degree
of nonnegative degree n and real argument 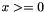 .
.
The Laguerre polynomial is defined by:
![\[ L_n(x) = \frac{e^x}{n!} \frac{d^n}{dx^n} (x^ne^{-x}) \]](form_49.png)
- Template Parameters
-
_Tp The floating-point type of the argument __x.
- Parameters
-
__n The nonnegative order __x The argument __x >= 0
- Exceptions
-
std::domain_error if __x < 0.
|
inline |
|
inline |
|
inline |
Return the Legendre polynomial 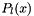 of nonnegative degree
of nonnegative degree 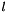 and real argument
and real argument 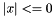 .
.
The Legendre function of order 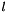 and argument
and argument 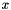 ,
, 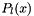 , is defined by:
, is defined by:
![\[ P_l(x) = \frac{1}{2^l l!}\frac{d^l}{dx^l}(x^2 - 1)^{l} \]](form_96.png)
- Template Parameters
-
_Tp The floating-point type of the argument __x.
- Parameters
-
__l The degree 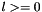
__x The argument abs(__x)<= 1
- Exceptions
-
std::domain_error if abs(__x)> 1
|
inline |
|
inline |
|
inline |
|
inline |
|
inline |
|
inline |
Return the spherical Bessel function 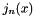 of nonnegative order n and real argument
of nonnegative order n and real argument 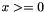 .
.
The spherical Bessel function is defined by:
![\[ j_n(x) = \left(\frac{\pi}{2x} \right) ^{1/2} J_{n+1/2}(x) \]](form_104.png)
- Template Parameters
-
_Tp The floating-point type of the argument __x.
- Parameters
-
__n The integral order n >= 0__x The real argument x >= 0
- Exceptions
-
std::domain_error if __x < 0.
|
inline |
|
inline |
|
inline |
Return the spherical Legendre function of nonnegative integral degree l and order m and real angle 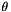 in radians.
in radians.
The spherical Legendre function is defined by
![\[ Y_l^m(\theta,\phi) = (-1)^m[\frac{(2l+1)}{4\pi} \frac{(l-m)!}{(l+m)!}] P_l^m(\cos\theta) \exp^{im\phi} \]](form_106.png)
- Template Parameters
-
_Tp The floating-point type of the angle __theta.
- Parameters
-
__l The order __l >= 0__m The degree __m >= 0and__m <= __l__theta The radian polar angle argument
|
inline |
|
inline |
|
inline |
Return the spherical Neumann function of integral order 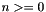 and real argument
and real argument 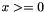 .
.
The spherical Neumann function is defined by
![\[ n_n(x) = \left(\frac{\pi}{2x} \right) ^{1/2} N_{n+1/2}(x) \]](form_108.png)
- Template Parameters
-
_Tp The floating-point type of the argument __x.
- Parameters
-
__n The integral order n >= 0__x The real argument __x >= 0
- Exceptions
-
std::domain_error if __x < 0.
|
inline |
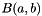 , for
, for 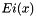 for
for ![\[ Ei(x) = -\int_{-x}^\infty \frac{e^t}{t} dt \]](form_89.png)
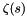 for real argument
for real argument 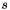 .
.![\[ \zeta(s) = \sum_{k=1}^{\infty} k^{-s} \hbox{ for } s > 1 \]](form_100.png)
![\[ \zeta(s) = \frac{1}{1-2^{1-s}}\sum_{k=1}^{\infty}(-1)^{k-1}k^{-s} \hbox{ for } 0 <= s <= 1 \]](form_101.png)
![\[ \zeta(s) = 2^s \pi^{s-1} \sin(\frac{\pi s}{2}) \Gamma(1-s) \zeta(1-s) \]](form_102.png)
